1. 论文概述
- 本文主要探讨在残差网络[1]一文中所使用的单位链接（Identity Mapping）在网络中的前向和反向传播性质
2. 具体分析
2.1 前向和反向传播性质
在[1]中的残差结构主要为
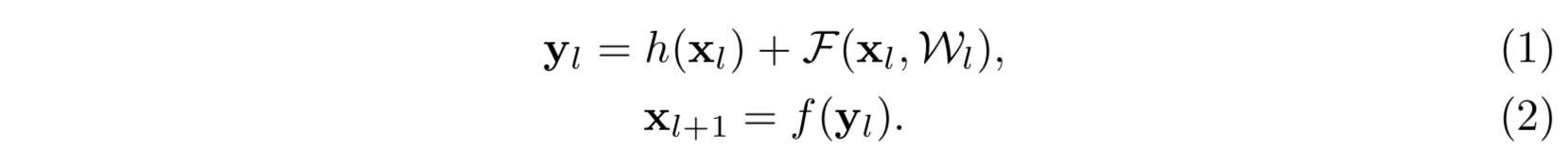
其中 $x_l, x_{l+1}$ 分别为第 $l$ 和 $l+1$ 层的输入，$f$ 是第 $l$ 层的激活函数，$h$ 则为单位映射即 $h(x) = x$，$F$ 为所需学习的残差函数。如果我们不妨简单得设激活函数 $f$ 亦为单位映射，则我们可以得到如下前向递推关系：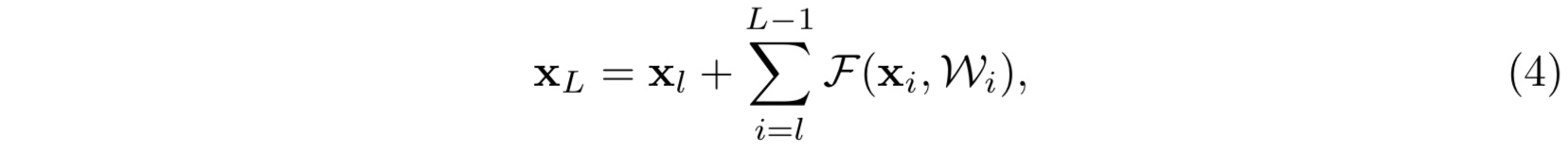
公式（4）有两点很好的（前向传播）性质：- 其中第二项加和项亦可以看作是第 $l$ 层和第 $L$ 层之间的残差（这一点十分优雅，这样的话堆叠残差块就没有看上去那么粗暴了）
- 第 $L$ 层的输入就等价于前面 $L-l$ 个残差模块的输出之和再加上第 $l$ 层的原始输入，这就区别于传统的神经网络（可以看作是 $L-l$ 个参数矩阵与原始输入的乘法）
公式（4）对于反向传播也有很好的性质：
- 记误差函数为大epsilon（这里打不出，记为E），则有反向传播如下：
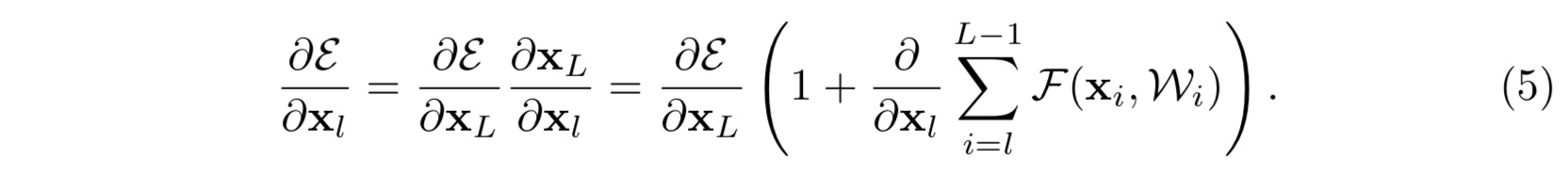
上式将梯度 $\frac{\partial E}{\partial x_l}$ 分解为两项之和，其中第一项为第 $L$ 层输入的直接梯度，第二项是中间各层的梯度之和，而前面一项正是保证了第 $L$ 层的梯度能够直接传到任意浅的第 $l$ 层 - 这样的一个梯度分解也可以很大程度上缓解梯度逐层传播而消失的问题，缘于分解中的后一项 $\frac{\partial}{\partial x_L}\sum_{i=l}^{L-1}F(x_i,W_i)$ 不可能在一个小批量中对所有的训练样本都等于 $-1$（这个可能有点主观）
注：公式（4）的前提是
- 单位链接
- 单位激活
故接下来将单独分析这两个前提对模型的影响。
2.2 单位链接的重要性
- 考虑另一种简单的情形：
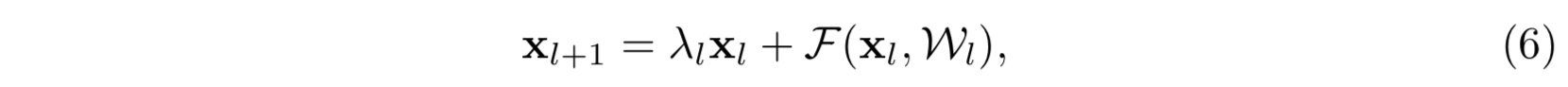
在这里我们仍然假设激活函数是单位激活函数，$f(x) = x$。那么公式（4）就相应地变为：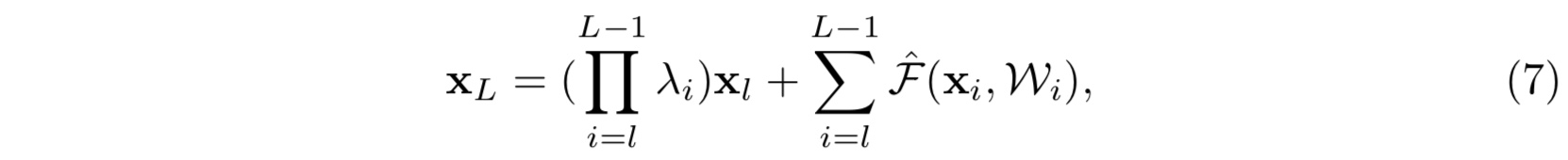
同样地公式（5）就变为：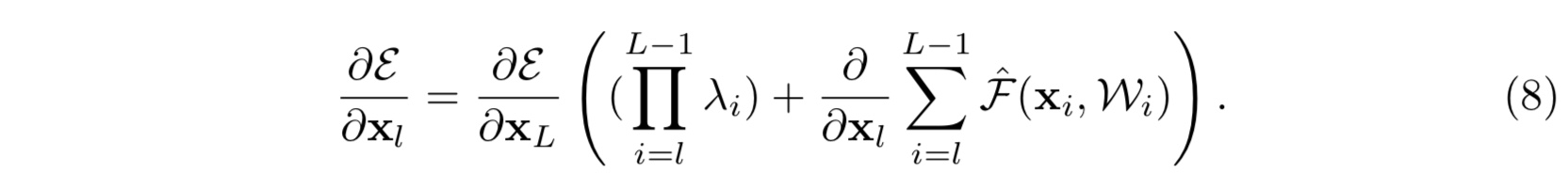
那么可以看出，如若第一项 $\prod_{i=1}^{L-1}\lambda_i$ 中的 ${\lambda_i}$ 有很多项或者全部大于 $1$，又或者小于 $1$，当网络越来越深， $L-l$越来越大的时候，则会使得这一项变得很大亦或者变得很小，接近于零而消失，都会使得模型的学习出现障碍，造成模型优化困难。这一点由实验佐证（具体见论文）- 注：
类似的跨层链接（shortcut connection）是一种信息传播很直接的方法，但是在其中加入一些复杂的操作例如（scaling,gating,1x1 convolution and dropout）会导致优化问题——即虽然增加了模型的表达能力（representation power）但是却很难优化模型，使得最后的结果反倒不如单位链接。
- 注：
2.3 激活函数的选择（跨层链接的结构）
下图是所有我们进行分析的一些跨层链接的结构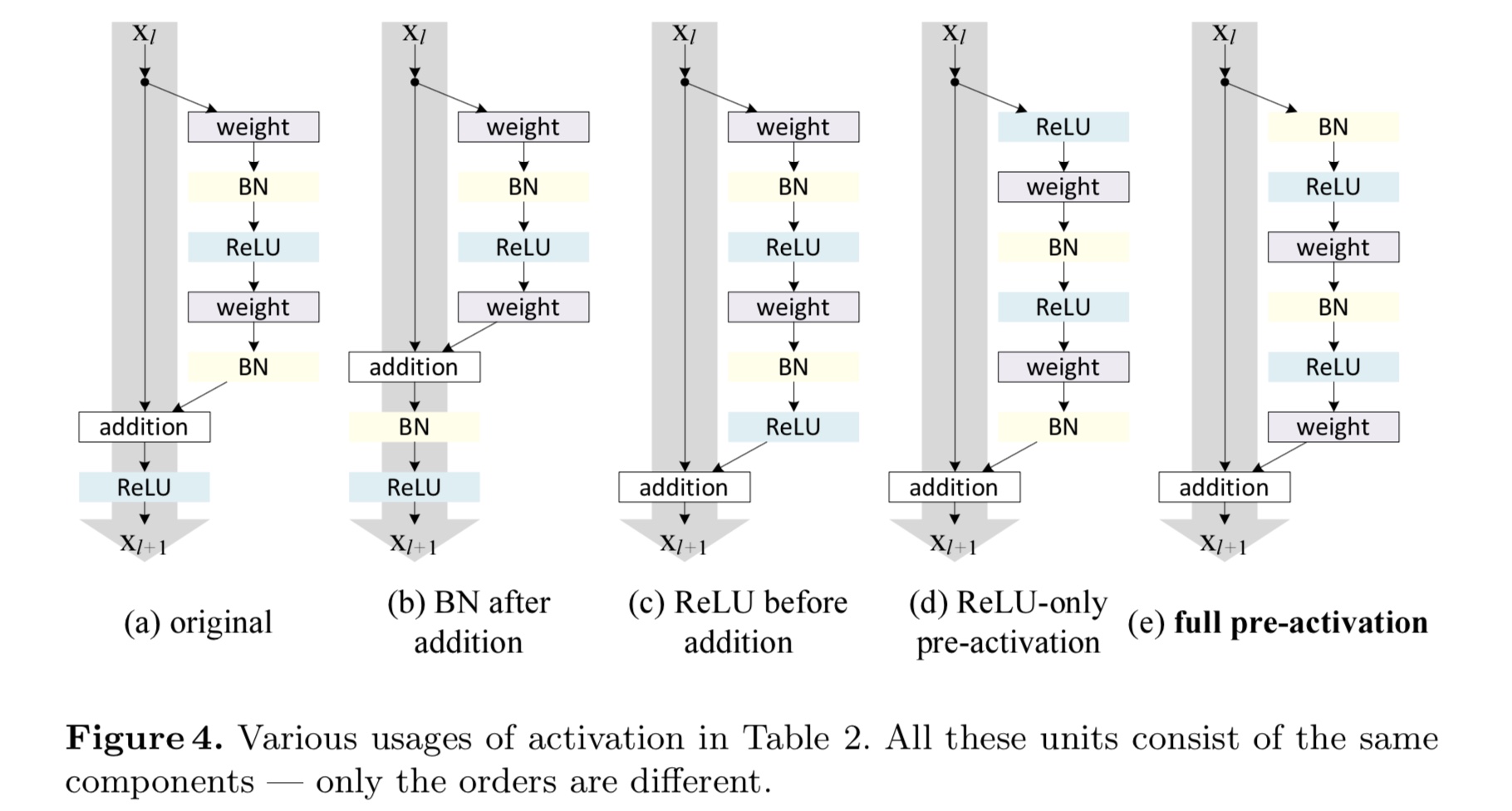
其中（a）是[1]中的默认设置。并且这里需要说明一点的是，如果激活函数使用了ReLU（也是实验中真的用到的，见（a）），那么之前那些公式的理论推导就相当于是一种近似。接下来我们主要探讨图（4）中的一些残差模块结构的变体。
- （b）BN after addition
这个表现很差，又回到了没有引入残差网络时的情况了 - （c）ReLU before addition
虽然这么做激活函数 $f$ 确实变成了单位映射，然而由于ReLU本身的非负性导致该情形下的残差是非负的，这与残差本身的意义不符。实验也表明了此变体的表现有所下降 - （d）Pre-activation or Post-activation？
在原始结构（a）中，激活函数 $f$ 不仅会影响下一个残差模块的输入，同时也影响到了下一个模块的跨层链接，也就是指：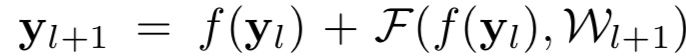
{:height=”50%” width=”50%”}
而（d）变体结构正是想要将这双重影响区分开来，从而变为：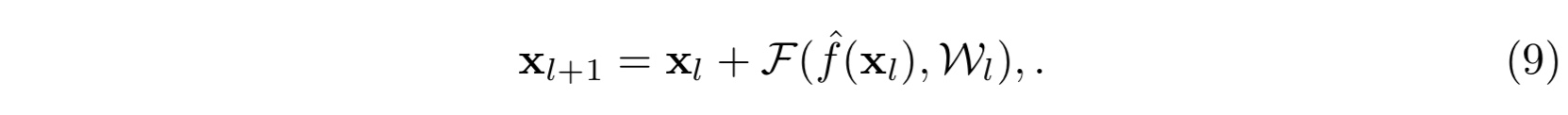
此时那激活函数 $f$ 也变成单位映射了。其实这里所讲的 pre-activation 或者是 Post-activation 指的是激活函数（ReLU或BN）相对于目标参数是先作用还是后作用。例如图（4）中（d）结构，ReLU是先作用于weight；（e）结构，ReLU和BN都是先作用于weight，这一点需区分于（a，b，c）结构。最后实验结果表明，（e）结构，当两者都先作用时表现最好。
2.4 进一步分析结构（e）full pre-activation
其带来的影响主要有两点：
此时的跨层链接是单位映射，故训练过程会更加容易
优先使用BatchNorm能够对网络起到正则化的效果
这一部分主要看实验结果。
