1. 论文概述
- 主要面对的问题
- 深度学习模型(神经网络)越深,越难训练
- 解决方案
- 提出了残差网络(residual learning framework),将学习‘未知函数’的任务转化为学习与输入的残差函数
- 实验表明残差网络更易训练,并且能够得益于更深的网络结构
2. 相关工作
- 残差表示(Residual Representations)
- These methods suggest that a good reformulation or preconditioning can simplify the optimization.
- 跨层链接(Shortcut Connections)
- 在残差结构(residual block)中,这种链接是单位链接(Identity shortcut connection),也就意味着没有参数;另一方面,如果将这部分链接的量置为0,该层网络结构也就与正常网络结构无异
3. 深度残差学习
3.1 残差学习
我们记 $H(x)$ 为所需学习的函数,其由一些连续的网络层(可以不是整个网络)所代表;$x$ 记为这些层最开始的输入。如果假设这些网络层能够模拟复杂函数 $H(x)$,那么同样地,我们也可以假设其可以模拟残差函数 $H(x)-x$,记为 $F(x)$,于是原函数就变为 $F(x)+x$。
- 动机
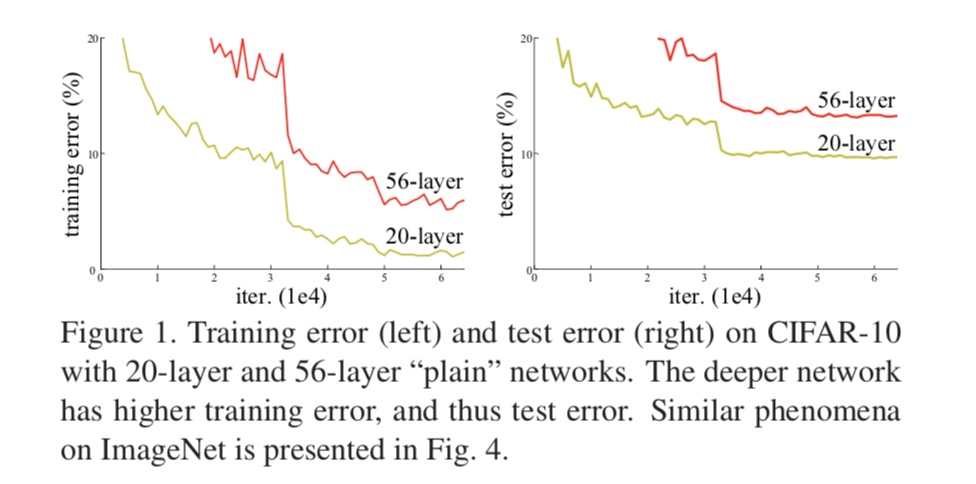
如图(1)左所示,更深的神经网络的训练误差反而明显高于较浅的神经网络,这是非常反直觉的——即使更深的网络层都学到的是单位映射,也应该与较浅的网络结构表现相同,也不至于差差这么多——这就暗示了多层非线性神经网络可能在学习单位映射时很困难。
现在有了残差网络这种重新的表示形式(reformulation),较深的层只需要将网络参数都置为0,即可学到单位映射(因为还有残差链接)。当然,在实际问题中很少有需要网络学习单位映射的情形,但是我们的残差网络可以帮助重新定义问题(即学习的目标函数改变了)。
- 残差模块(residual block)
最典型的残差模块如下图所示: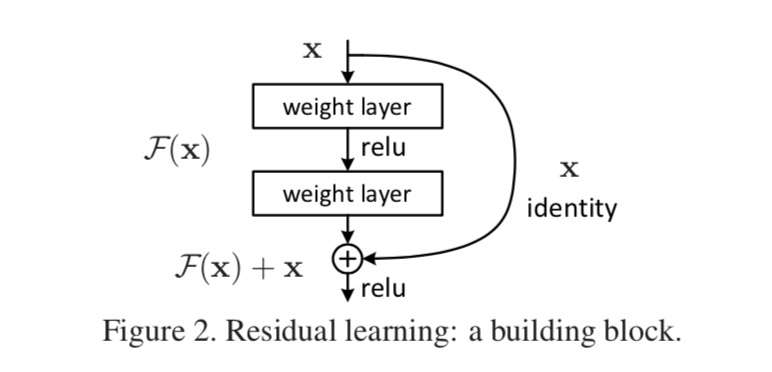
输入和输出定义为:
$$
y = \mathcal{F}(x, {W_i}) + x
$$
这里的“+”即为对应元素之和(参考矩阵加法);并且这里潜在要求 $y$ 和 $x$ 具有相同的纬度和尺寸,否则可以用一个线性映射来进一步调整残差的纬度和尺寸以符合输出:
$$
y = \mathcal{F}(x, {W_i}) + W_sx
$$
注:此处 $W_s$ 当然可以是一个矩阵作为残差网络的一组参数进行学习,但是实验表明单位映射已经表现得足够好并且又十分高效简洁。

