源代码:Github,欢迎加Star,里面包括完整英文report
阅读要求:了解红黑树的基本性质及插入删除操作。
这是我在CMU课程15-618(Parallel Computing)中的期末项目,由我和室友两人完成,室友主要负责插入操作,我主要负责删除操作,后面我们会看到,这两个操作的区别。我们基于C++中的CAS(<atomic>.compare_exchange_weak)实现了细粒度的线程安全红黑树结构,支持多线程插入和删除,并且在多核CPU上达到了线性加速比的效果(测试数据量为10w,线程数最多为16个)。
整个的算法思想主要参考这篇论文,我们可以说是修正并完善了该论文提出的算法流程,并且是全网第一个该论文的正确开源实现(Github上有两个能跑的实现,rutvij93 和 josecamacho8,前者是随着线程数增大反而变慢,而后者是仅仅在非常小的数据量级上进行实验甚至还会出现死锁情况)。
之所以说我们是修正并完善了该论文提出的算法流程是因为原论文中虽然有着看似很详尽的伪代码,但其实在一些重要的函数内,作者却省略了关键的步骤,甚至伪代码之间还有冲突。原论文并没有实验数据就很好地说明了作者自己并没有一个正确实现的版本。
1. 关于红黑树
关于红黑树的概念以及(单线程)插入和删除的算法流程在《算法导论》中已经阐述得很详尽了,这里就不再赘述。不过一个有趣的问题是——为什么业界的很多自平衡树的实现(例如C++ STL的map和set,Java的Hashmap当节点链表长度大于8的时候,Linux内核等等)都是清一色的红黑树而不是选择平衡性更高的AVL树呢?
起初,我也是想当然得认为,AVL树由于平衡性更严格,所以在插入和删除时所需要作出的调整就会相比于红黑树更多,所以性能会有所下降。一个最普遍的说法是
AVL树和红黑树插入节点的时候均需要
O(1)次旋转操作,而当删除一个节点时,AVL树最坏需要O(logN)次旋转而红黑树仍然只需要O(1)次旋转。
但真的是这样吗?其实不然。
【具体内容后续补充,先跳过】
2. 符号及相关概念
2.1 符号定义
为方便后文的表述,有必要先来定义一些符号如下。
x,在插入/删除阶段的目标节点p,x的父亲节点w,x的兄弟节点gp,x的祖父节点u,x的叔叔节点,也即p的兄弟节点wlc,w的左儿子节点wrc,w的右儿子节点flag,每个节点对象中的一个布尔变量,变量为真表示当前节点已经被一个线程标记marker,每个节点对象中的一个整型变量,变量的值代表了线程ID
2.2 flag变量和CAS操作
需要特殊说明的是,flag是一个C++的原子类即atomic<bool>。原子类有一个成员函数std::atomic::compare_exchange_weak(),这就是我们实现所用到的CAS操作。而marker不需要CAS操作,因为整个算法流程保证了一个线程会先获取节点的flag,才会设置marker。所以每个节点的flag就是线程同步的关键变量,可以理解为锁,只是在这里的锁并不满足请求与保持条件——即如果请求资源阻塞,则会主动释放已获取的资源,也就是Lock-free的思想。
compare_exchange_weak和compare_exchange_strong的区别会涉及到硬件层面。简单来说,即使需要比较的值是一样的,即满足交换条件,compare_exchange_weak仍有可能返回false,而compare_exchange_strong则保证会返回true。所以在实践中,如果本身就需要自旋的话,用weak的效率会高一些,而如果不需要自旋的话,strong可能是更好的选择。
注:对于红黑树来说,不论是插入还是删除,最麻烦的部分都是插入或删除节点之后对树进行自下而上的调整以保持红黑树的性质。因此下文中说的插入和删除操作也主要指的是这些调整操作。
2.3 局部区域(local area)
这个名词可能有些奇怪,但是暂时没有想到更合适的词语,就采用直译吧。这个概念是[1]中作者提出的,局部区域的定义是在插入和删除过程中的一次操作所需要涉及的一些关键节点的集合。
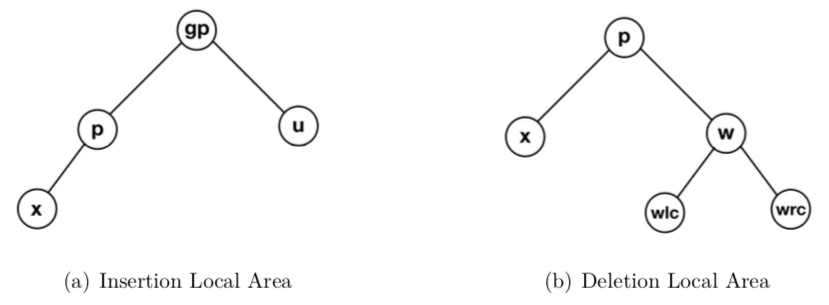
如上图所示,插入操作的局部区域包括x, p, gp, u,删除操作的局部区域包括x,p,w,wlc,wrc。在一个线程进行插入或删除操作之前,它需要先占有这个局部区域内所有的节点,而这个占有是有顺序的,其顺序就是上面所列出的顺序。
3. 算法实现
3.1 搜索
在讲插入和删除之前,不妨先来看看相对简单的查找是如何通过CAS操作实现线程安全的。
这里用到的思想比较简单直接,即hand-over-hand locking。主要步骤为
- 自旋获取根节点的
flag - 如果当前节点的
value是查找的值,则查找结束,返回当前节点 - 根据二分查找的顺序通过CAS获取下一个节点的
flag - 如果CAS失败则释放父节点的
flag,然后重新从根节点开始 - 如果获取成功且当前节点非叶子结点(红黑树中,所有的叶子结点均为
null),则释放父节点的flag - 重复步骤
2~6
代码如下:
tree_node *par_find(tree_node *root, int value)
{
bool expect;
tree_node *root_node;
restart:
do {
root_node = root->left_child;
expect = false;
} while (!root_node->flag.compare_exchange_weak(expect, true));
tree_node *y = root_node;
tree_node *z = NULL;
while (!y->is_leaf)
{
z = y; // store old y
if (value == y->value)
return y; // find the node y
else if (value > y->value)
y = y->right_child;
else
y = y->left_child;
expect = false;
if (!y->flag.compare_exchange_weak(expect, true))
{
z->flag = false; // release held flag
usleep(100);
goto restart;
}
if (!y->is_leaf)
z->flag = false; // release old y's flag
}
return NULL; // node not found
}注意这里的root并不是实际意义上的根节点,只是为了方便处理边界问题而引入的一个节点,实际意义的根节点是root->left_child。并且也可以看到其中贯彻了lock-free的思想,即一旦获取资源失败,则释放当前资源/状态。可以说整套算法几乎就是CAS+lock-free。
3.2 插入
本节中3.3.1部分的图片来源于红黑树(一):插入。
由于红黑树中作为NULL指针的叶子节点要设为黑色,因此实现中为了方便,将叶子节点实体化为一种特殊类型的节点来让其包含颜色,而不是用NULL指针表示。
3.2.1 单线程下的插入处理
先来看看单线程下的插入操作是怎么处理的。首先构建一个新节点,将其设为红色,然后像对待二叉搜索树一样进行插入操作(搜索直到遇见叶子节点(NULL指针),把新节点放到NULL指针的位置),最后进行一系列旋转+染色操作让树重新遵守红黑树的规则。为什么要将新节点设为红色?Robert Lafore在Data Structures & Algorithms in Java Second Edition给出了三点原因:
- 红黑树要求任意路径的黑色节点数量相等,那么插入红色节点不会影响这条rule。
- 当然,红黑树也不允许两个连续红色节点,但插入红色节点破坏rule的可能性更低。(插入黑色节点一定会破坏1中的rule,但插入红色节点有一半的概率不会破坏rule,因为只有在其父亲节点为红色时才会破坏rule)
- 修复两个连续红色节点要比修复黑色节点数量不等更为容易。
插入后有两种case不需要进行修复:
- Trivial Case#1:新节点是根节点。直接将其设为黑色即可满足条件。
- Trivial Case#2:新节点的父亲节点是黑色。这意味着新插入的节点没有打破红黑树规则,不需要修复。
这意味着只有在新节点的父亲节点为红色时才需要进行修复。而这种情况又可以根据其叔叔节点与兄弟节点的颜色细分成三种case:
Case#1:叔叔节点为红色,情形如下图(a)。我们可以通过将P和U设为黑色,G设为红色来让这四个节点符合要求,但G染红也可能导致红黑树规则被破坏。那么我们可以将G当作新插入的节点,对其递归地进行case的判定以及对应的修复。
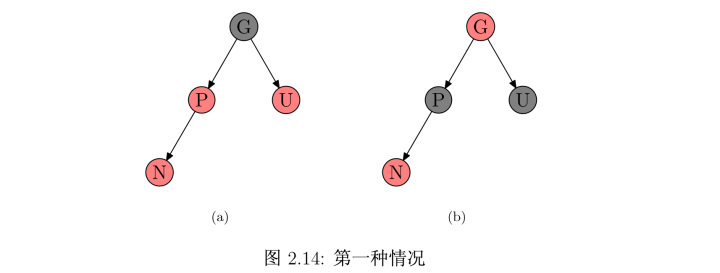
Case#2:叔叔节点为黑色,且N为P的左儿子,情形如下图(a)。那么将P右旋,并交换P与G的颜色就能恢复,最终如下图(c)。(这个操作可以看成先染色再旋转:为了避免连续红色节点,交换P与G的颜色;而染色导致G的左子树路径上黑色节点比右子树多一,因此将P右旋,把黑色的P从左子树独占变成两子树的共同节点。)
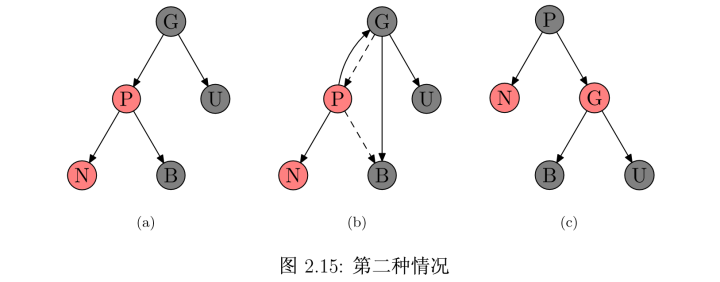
Case#3:叔叔节点为黑色,且N为P的右儿子,情形如下图(a)。此时要先将N左旋,再将N右旋,最后交换N和G的颜色,最终如下图(c)。(这个操作也可以看成先染色再旋转:首先为了避免连续红色节点将N染黑,然后P的右子树比左子树多一个黑色节点,因此将N左旋变为两者共同节点。而此时G的左子树自身平衡了,但比右子树多了一个黑色节点,所以将N右旋,提升成两子树的共同节点。最后发现右子树比左子树多了一个黑色节点,由于N-G-U是三个连续黑色节点,因此可以把G染红。)
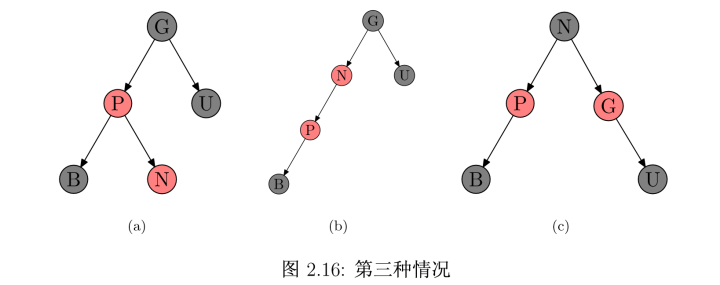
注:以上图中N是P的左/右儿子会影响case的判定,但P是G的左还是右儿子不会影响。
3.2.2 多线程下额外的考虑
多线程下首先要改动的就是搜索的过程。这里插入节点的部分用到了上面3.1所说的Hand-over-hand方法,最终找到叶子节点后用新节点替换。
而修复的过程也需要获取flag来避免竞争。上面共总结出了5个Case,其中除了Case#1以外,都是只需要对图中这五个节点进行操作就可以了。所以基本思想就是插入后把这五个节点的锁都占上,等修复操作结束后再释放,而这五个节点也就是上面提到的局部区域(插入版)。
麻烦之处在于Case#1:除了这五个节点外,它还有可能需要递归地操作更上面的节点。所以还要提供move_inserter_up的操作,获取图中gp(G)作为新插入节点所对应的local area,包括额外四个节点的flag。新的local area建立之后,才能对gp(G)进行下一步判定和操作。
3.2.3 插入流程图
插入的流程图如下所示。白色的部分对应着插入新节点的操作,橙色的部分是插入后修复红黑树结构的操作,对应于insert fixup。蓝色的部分则是与local area相关的操作,每个线程在开始修改结构前需要建立local area,获取相关节点的flag,并在修复完成后释放这些flag。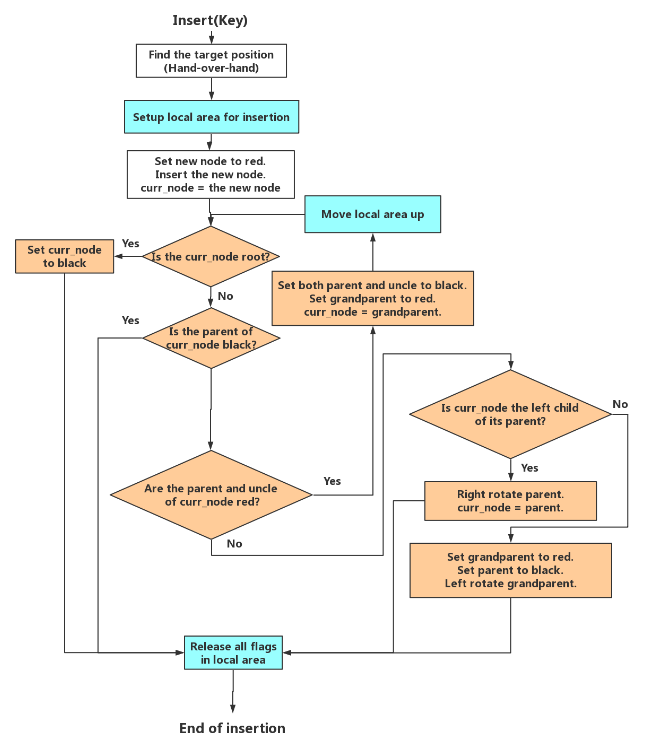
3.3 删除
3.3.1 死锁避免
1. 为什么会死锁
在正式介绍插入和删除的具体流程之前,我想先谈谈死锁的问题。目前为止,我们只提及了局部区域和CAS获取flag的机制,但是仅仅依靠这两个机制并不能够让我们的算法避免死锁问题。因为在红黑树的删除过程中,x是可能会上移的,这就意味着此时我们需要以新的x为起点重新获取局部区域的所有flag,并且由于此时删除操作没有完成,更关键的是,在那个情形下,将红黑树的状态恢复到该删除操作之前已经不可能了。因此,一旦一个线程成功获取了最初的局部区域并开始进行删除操作,那么这个删除操作就不可撤回。特别的,在整个调整完成之前,x的flag是不可能释放的(x只可能上移)。所以,从这个意义上说,我们的算法是阻塞性的。而阻塞性质就会带来下面这个死锁情形:
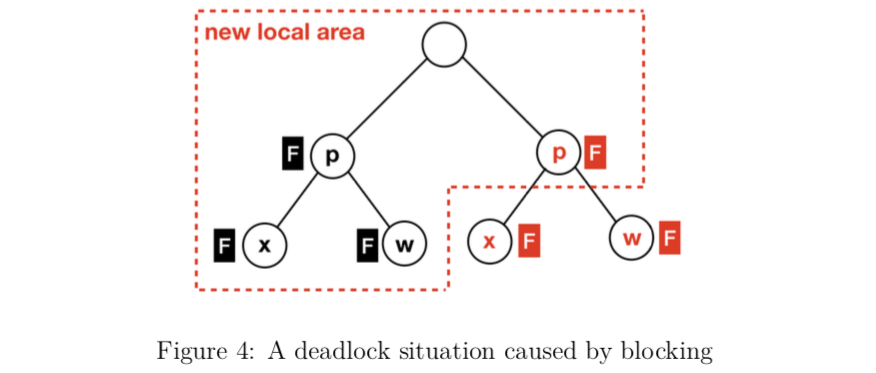
这个情形中,黑色和红色线程均已经获取了x, p, w的flag,而当红色线程中的x需要上移时,红色线程所需的新的局部区域就变成了图中所示的五个节点,其中就包括了黑色线程已经占有的三个节点,最关键的是黑色线程的x节点,因为我们刚刚提到过,黑色线程不会释放x的flag。这就形成了典型的死锁。
注:只在删除过程中才会发生x节点需要上移的情况,因此上述死锁问题也仅会在删除过程中发生。
2. 如何避免死锁
上面这个案例并不是特例,在整个并行红黑树的算法流程中,发生死锁的风险均来自于两个线程离得过“近”,即两个线程的局部区域离得过“近”。因此,如何保证任意两个线程之间总是保持一个适当的距离是避免死锁的关键。那么剩下的问题就是——用什么机制保持距离?保持多“远”的距离?
Kim等人为此引入了marker的概念,来防止任意两个线程距离过近。其核心思想是——一个线程必须获取节点p以上的四个父辈节点的marker才能够正式开始删除操作。当然,在获取marker之前,仍需先获取相应的局部区域。
如果说flag可以看成锁的话,marker可以看作是一个比flag优先级低的锁。即一个线程能获取一个节点的flag当且仅当该节点的flag没有被其他线程获取。而一个线程能获取一个节点的marker当且仅当该节点的marker和flag均未被其他线程获取。
通过下图就可以看到,此时黑色线程已经获取了p以上的四个marker,而如果此时一个距离较近的红色线程想要获取它的四个marker时,就会在蓝色节点处失败。这也就意味着在黑色线程的删除操作结束前(或者黑色线程已经上移到蓝色节点之上),距离较近的红色线程不会开始删除操作。这样就保证了任意两个线程不会在处于较近的时候同时进行删除操作,也就避免了死锁情况。
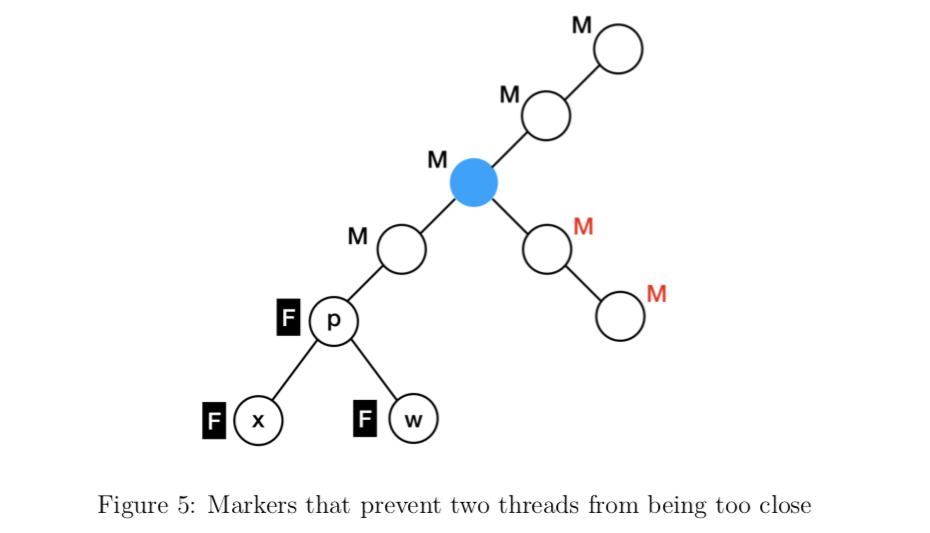
因此在正式开始删除之前大致可以分为四步:
- 经过类似3.1中的搜索过程找到目标节点,记为
y节点 - 遵循二叉搜索树删除原理,找到相应的后继节点
x - 获取
x节点的局部区域 - 获取
x的父亲节点p以上四个父辈节点的marker
这部分代码如下所示
// 在正式开始删除前的准备工作
restart:
//********* Step 1. 找到目标节点y *********//
tree_node *y = par_find(root, value);
tree_node *x; // 后继节点,即实际删除节点
if (y == NULL)
return;
//********* Step 2. 找到后继节点x *********//
if (y->left_child->is_leaf || y->right_child->is_leaf)
x = y;
else
x = par_find_successor(y);
if (x == NULL)
{
y->flag = false;
goto restart; // 获取x失败,从头来过
}
//********* Step 3&4. 获取x的局部区域以及相应的四个marker *********//
if (!setup_local_area_for_delete(x, y))
{
x->flag = false;
if (x != y) y->flag = false;
goto restart; // 获取flag/marker失败,从头来过
}其中值得一提的是15~19行部分的代码,之所以par_find_successor(y)可能会返回NULL是因为在获取后继节点的过程中,可能会失败的情形(例如遇到了另一个线程的局部区域)。并且在par_find_successor(y)函数内部失败重试的话可能会导致与另一个线程产生活锁(livelock),因为此时还未能保证这两个线程离得足够远。因此par_find_successor(y)失败的话,需要在上层逻辑进行失败重试,即``15~19`行。
3.3.2 删除流程
整个删除操作的流程图如下所示。其中白色部分是单线程红黑树原有的步骤(当然实现细节是有很大差异的),彩色的部分是为了线程安全而增加的步骤,并且remove fixup本身又是一个流程。
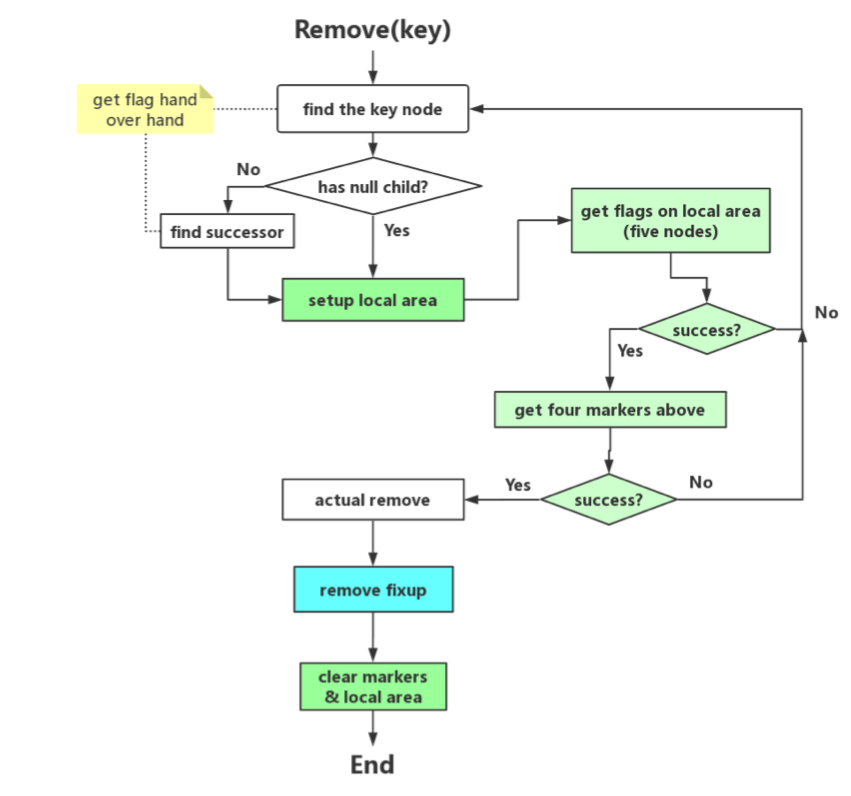
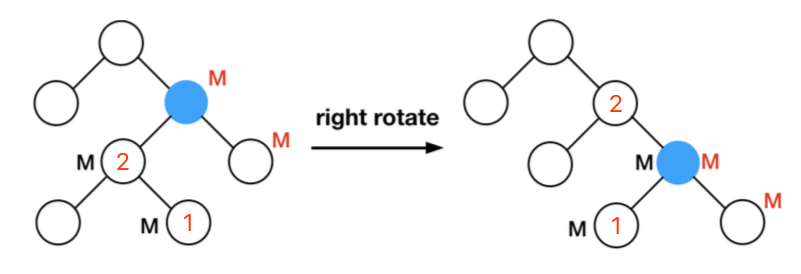
3.3.3 简化的marker机制
在原论文中,作者对marker机制的限制是,在进行节点左旋和右旋操作过程中,marker需要按照新的父子关系进行变更,即如下图所示。在对蓝色节点进行右旋操作后,1号节点的父亲节点由2号节点变成了蓝色节点,根据原论文的规定,此时原先黑色线程在2号节点的marker需要转移到蓝色节点上。这就导致了双重marker的问题,即蓝色节点同时包括黑色线程和红色线程的marker。这就破坏了marker的互斥性。而原论文中也引入了另外两个机制来解决这个问题,这里就不再赘述了。
重点是,我发现双重marker问题的根源是作者在节点左旋和右旋过程中对marker的处理,在具体实现中我发现完全可以将marker机制简化,从根本上就避免双重marker问题:
- 在左旋和右旋过程中,如果发现所牵涉的节点含有某个线程的
marker,则对其进行清除 - 线程的目标节点
x在每次需要上移前都需要再次获取四个父辈节点的marker以保证安全的距离
其中第一点可以做到是因为在旋转过程中,该线程必然已经获取整个局部区域。再加上marker机制,保证了一个旋转操作涉及的节点不会横跨两个局部区域,因此是线程安全的。
关于第二点,在原论文中,每次目标节点上升,只需要在原先的marker基础上,再多获取一个额外的marker即可。而在简化后的情况下,该线程则需要重新获取全部四个marker。因为在原论文的情况下,线程一旦获取了四个marker可以保证,在线程主动释放前,这四个marker会一直存在。但是在简化后的情况下,这四个marker可能会受到旋转影响被清除,因此每次目标节点上升时都需要重新获取四个marker。这一步可能相比原论文会略显复杂,但是简化后的marker机制所带来的收益也是很大的——从根本上避免双重marker问题,因此也不需要原论文提出的另外两个机制支持。
3.3.4 活锁问题
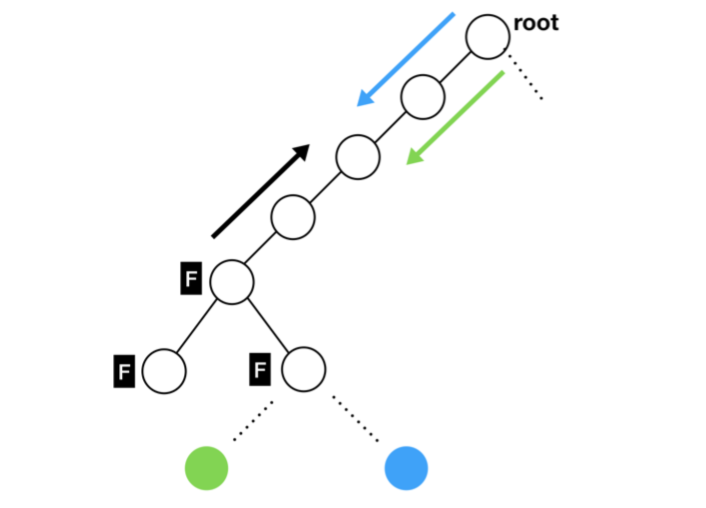
在3.2.1中提到删除操作是阻塞的(获取局部区域后),因此一个典型的活锁场景如下所示。其中黑色线程的目标节点企图上升,而此时另外有一个绿色线程开始搜索,其目标节点在黑色线程局部区域的子树部分。因此由于阻塞性,我们可以知道在黑色线程完成删除操作之前,绿色线程是不可能搜索到它的目标节点(绿色)的。在这种情况下,绿色线程会一直进行尝试。而由于黑色线程需要上升,因此它需要向上获取四个marker。当此时黑色线程的p节点与root节点过近时,活锁就会发生。此时有一个好消息和一个坏消息。好消息是这样的活锁状态并不是稳定的,即黑色线程有机会先于绿色线程获取四个marker后进而产生实质性的工作。坏消息是,如果类似的绿色线程很多,比如又有一个蓝色线程如图所示,那么活锁的概率就会大大增加。
在实际实现中,我发现只要让绿色线程、蓝色线程此类的线程在失败后,稍微进行一段时间的等待(约100us),就可以“解决”活锁问题。当然,这样的解决方法并不是像先前的死锁避免那样彻底解决该问题。但是,在后续测试中发现这样做的实际效果是足够好的。
5. 小结
这里的篇幅有限,没能把实现中的所有方面都阐述到,如果你有兴趣,欢迎查看源代码和阅读完整英文report。在英文报告中,我们也详细记录了我们的测试结果,其中还包括我们实现的另一个细粒度锁的红黑树插入版本,之所以没有实现细粒度锁的红黑树删除版本是因为本质上,如果不在失败后释放资源,是不能避免局部区域间的死锁问题的,因此从这个意义上来说,细粒度锁版本的删除操作是不可行的。又或者说,我们这里的删除操作也可以称为在失败后会放弃资源的细粒度锁版本。
参考
[1] Ma J. Lock-Free Insertions on Red-Black Trees[J]. Master’s thesis. The University of Manitoba, Canada October, 2003
[2] Kim J. H., Cameron H., Graham P. Lock-free red-black trees using cas[J]. Concurrency and Computation: Practice and experience, 2006: 1-40.
[3] compare_exchange_weak vs. compare_exchange_strong
[4] std::atomic

